Interactive simulation with Duty Cycle modification

Download Python Notebook

This python script example helps to understand how to change the value of a parameter during the simulation interactively (pseudo real time).

In this case, the duty cycle of a Buck converter will be modified suddenly at any time and the impact of this change will be observed on the output voltage through an oscilloscope.

The library called ipywidgets is used to create this interactive display in pseudo real-time.

This parameter modification is really useful to observe interactive change.

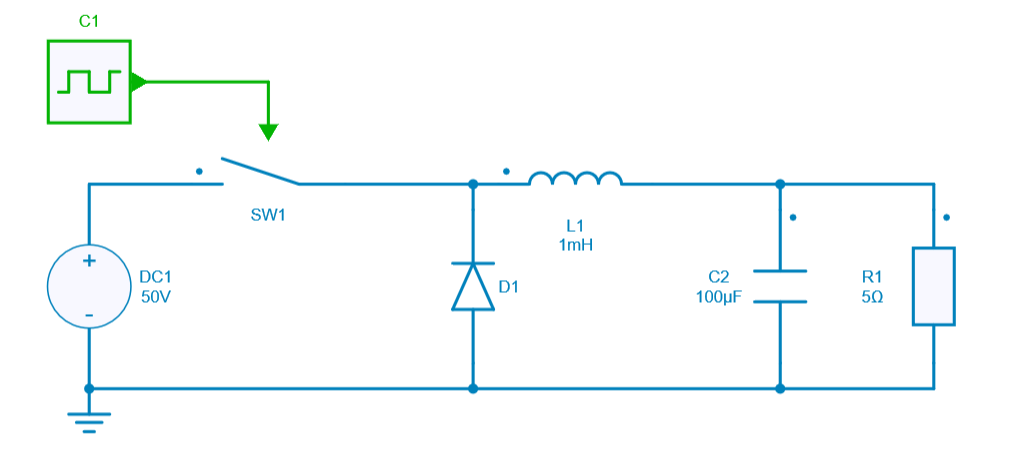
SIMBA circuit

Below the DC-DC power converter designed inside SIMBA Desktop.

Python Script

The Python script used for showing the interactive modification of duty cycle during simulation will do the following tasks:

• import all the necessary libraries including ipywidgets
• load the DC-DC Buck converter from SIMBA design examples
• create two array table_t and table_Vout
• enable both voltage and current scopes for $R_1$ parameter (load resistor)
• define a number of points (here 1000) which represents the intermediate time allowing to set up the sudden change of the duty cycle value. This set of points needs to be modified in order to change this “intermediate time”.
• define a function called run_simulation allowing to retrieve the duty cycle, time and output voltage, add datas to the 2 arrays created previously and refresh thoses arrays once their limits have been reached
• plot the output voltage through an oscilloscope + display a slide bar which allows to modify the duty cycle value during the simulation

Conclusion

Below the result of the output voltage once the simulation is over through the Python script:

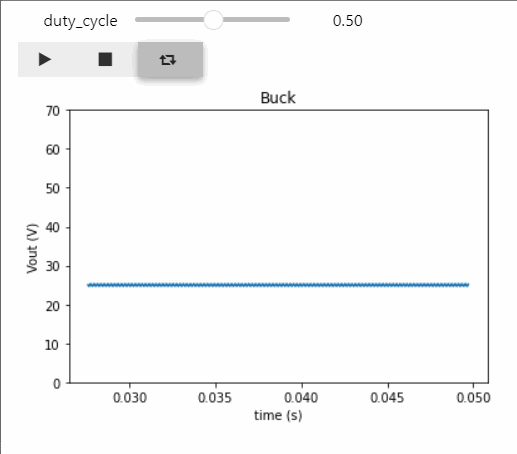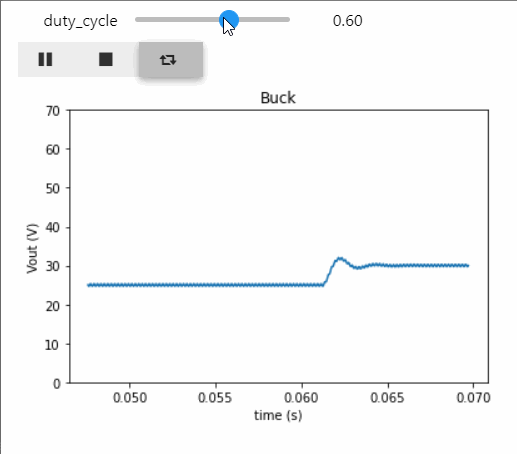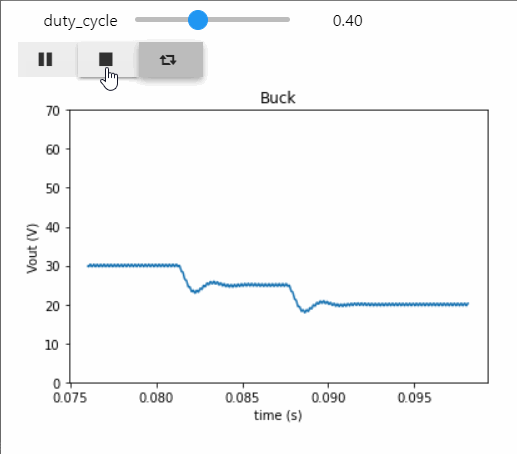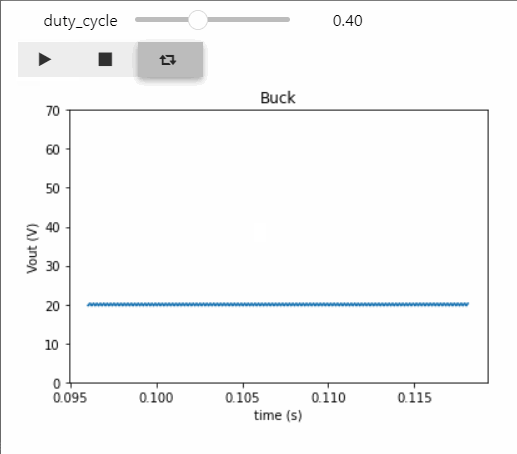
By using the ipywidgets library, we can: * create a slide bar displaying the duty cycle and play with its value * display 3 buttons in order to run/pause, stop and simulate with no end the simulation * display the output voltage and check the impact of duty cycle modification interactively

The output voltage can be directly calculated by using the theoretical calculation about Buck converter:

$V_{out} = D \times V_{in}$ where $D$ is the duty cycle.