Skip to content

Using the C-Code block

This tutorial covers the C-Code block in Simba.

This feature can help you to:

  • Implement custom controller with C code
  • Implement any mathematical equation

How to use the C-Code block?

To describe this feature, we consider the "C_block_RMS" circuit example.

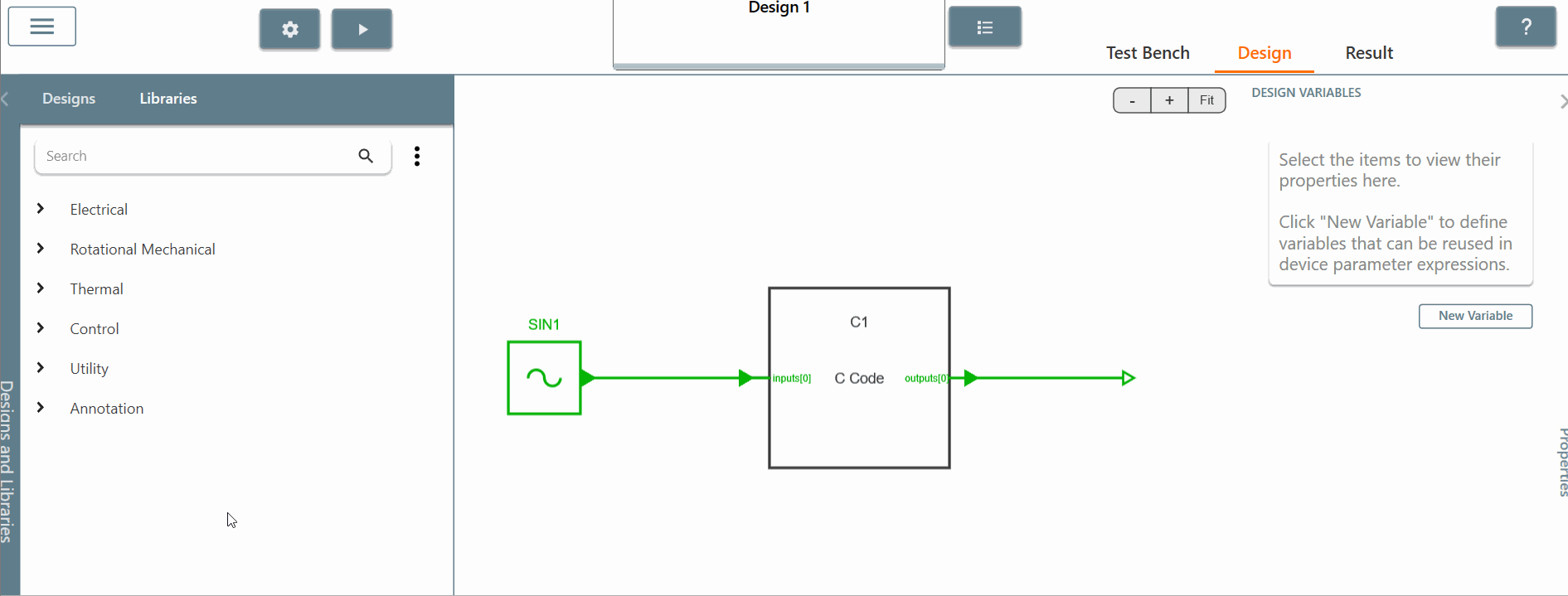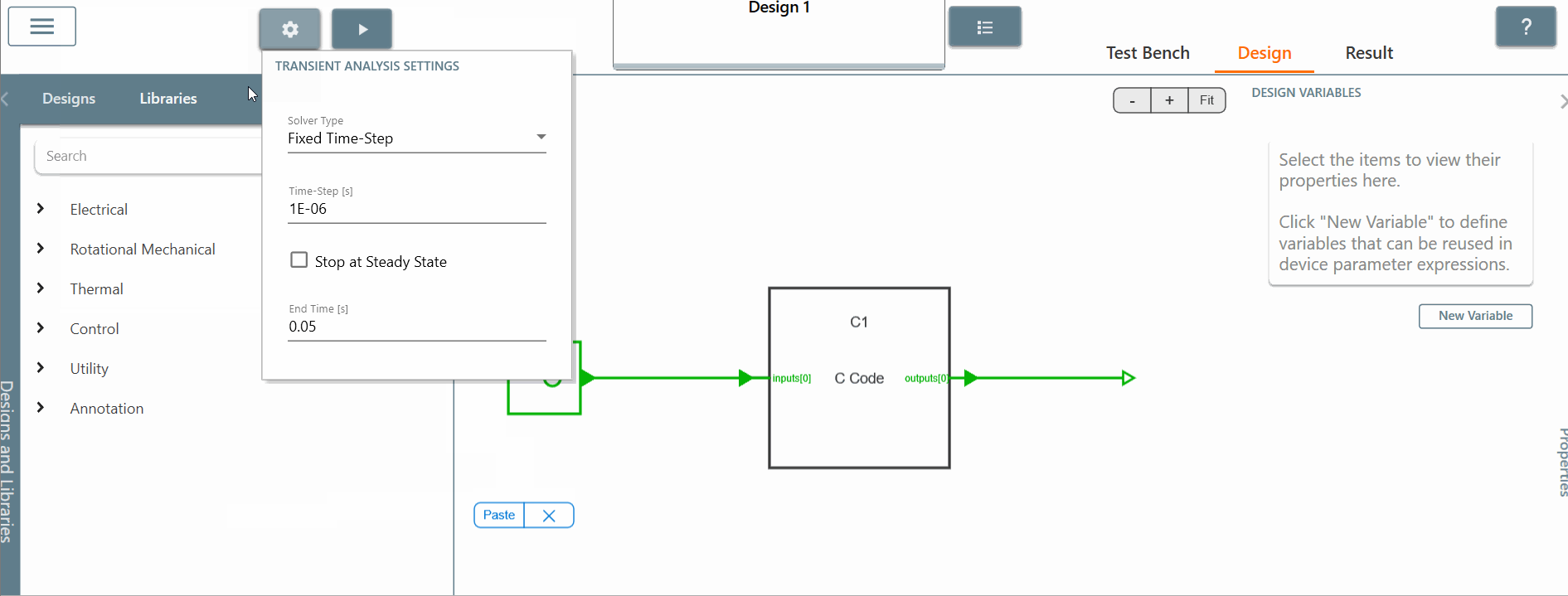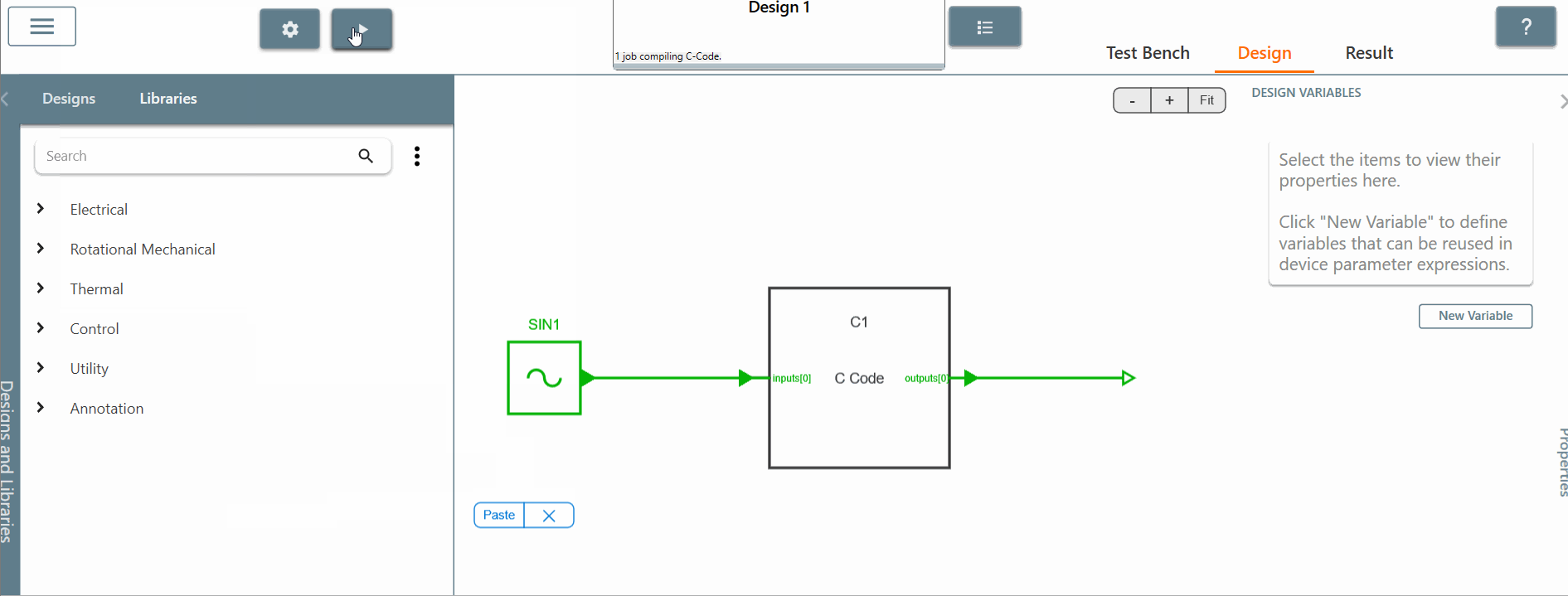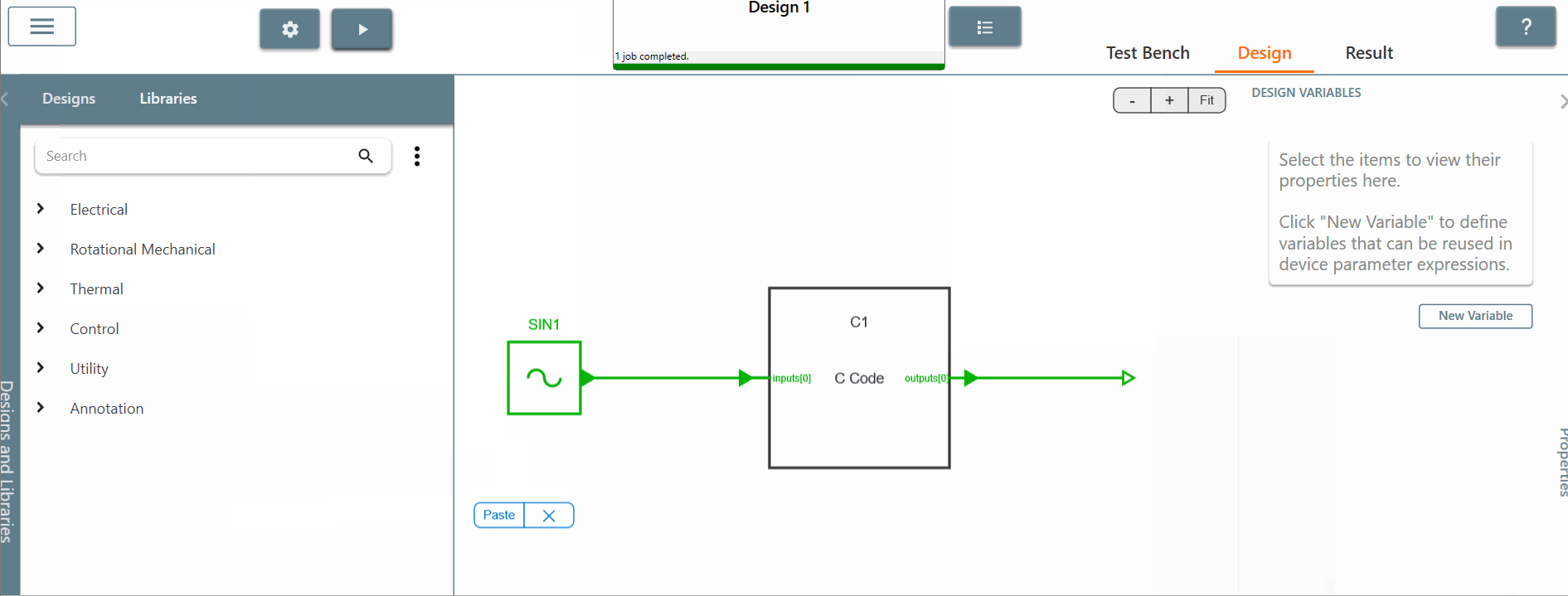
✔ Step 1: First, we will configure the "Transient Analysis Settings" from the "wheel" icon.

wheel

If you click on this icon, you will see:

  • Solver type: we set it to "Fixed time step". The C Code bloc can also be used with the predictive time step feature.

  • Time step: keep "1E-06".

  • End time: set it to "0.05".

wheel

✔ Step 2: Next, we will build the circuit to calculate the RMS value of the sinusoidal input source using the C block.

✔ Step 2.a: Choose and place a "sinusoidal control source" in the library and set the amplitude equal to 1 and the frequency equal to 60 Hertz.

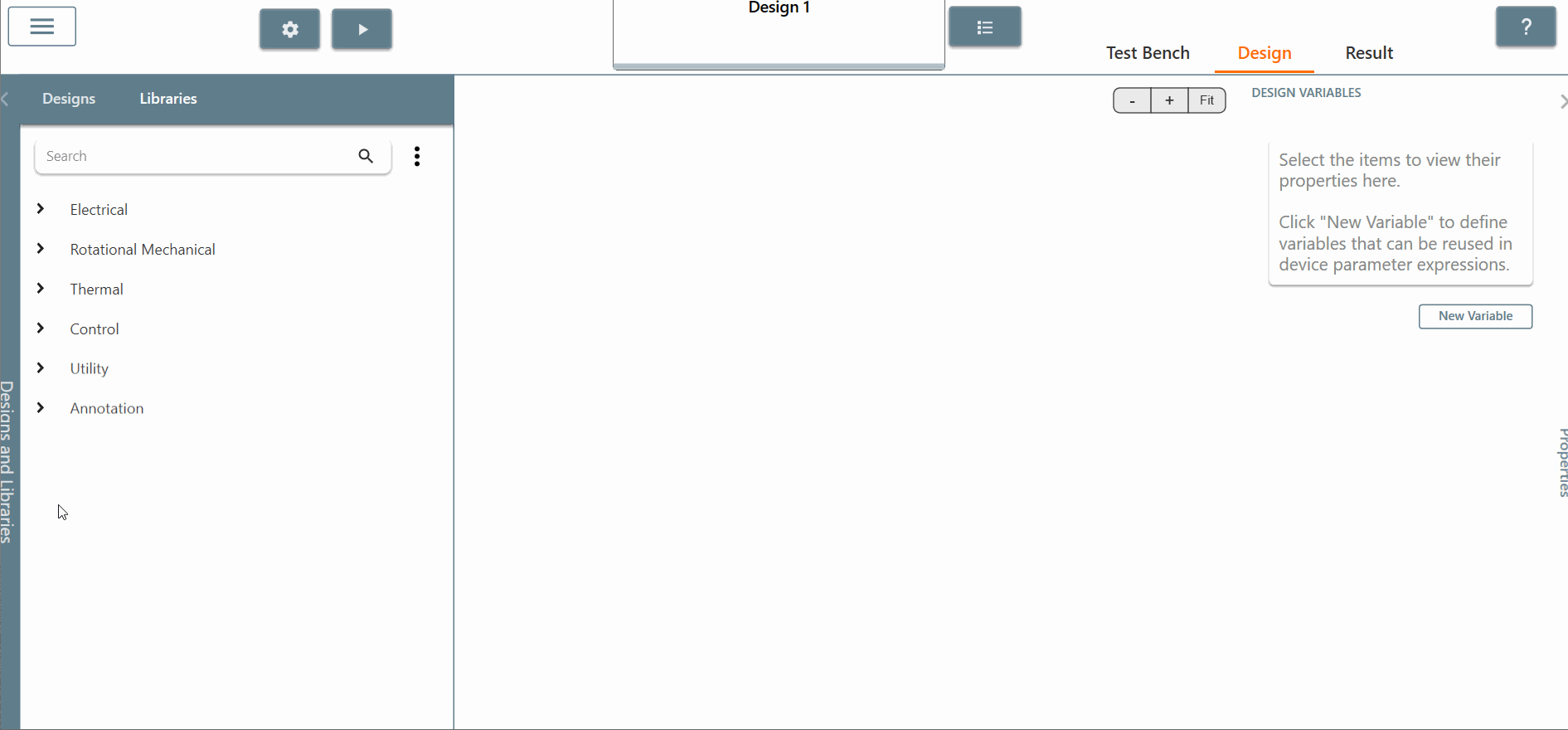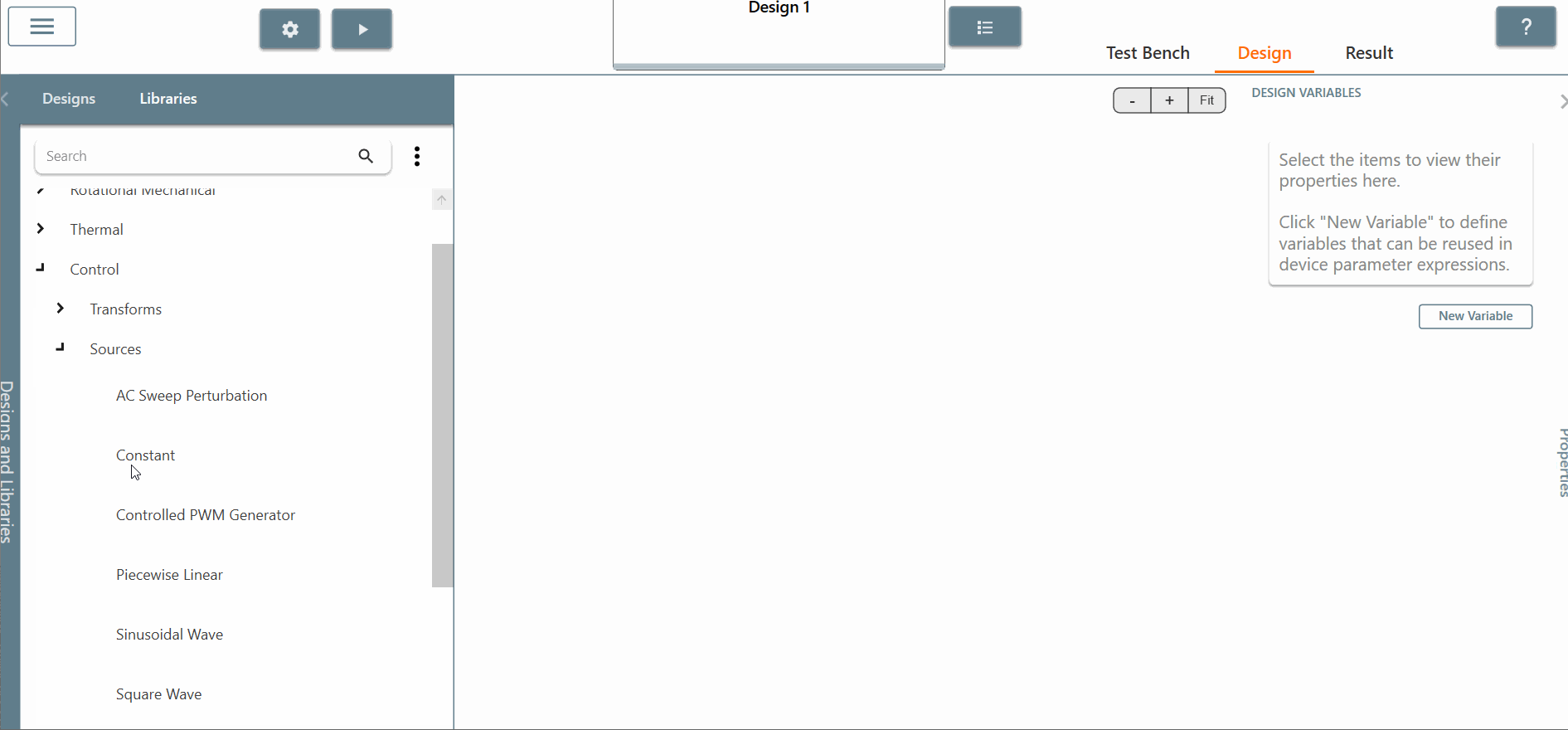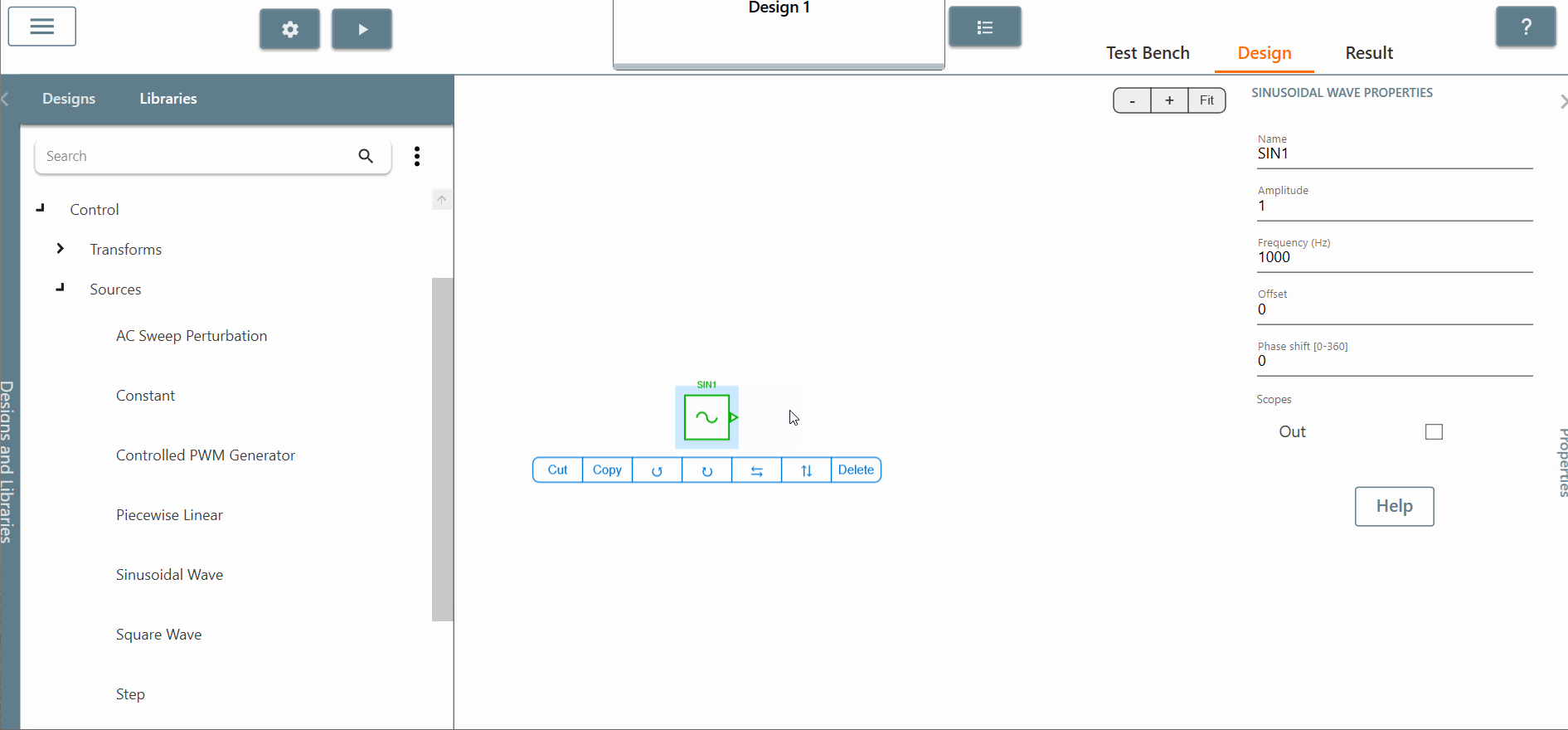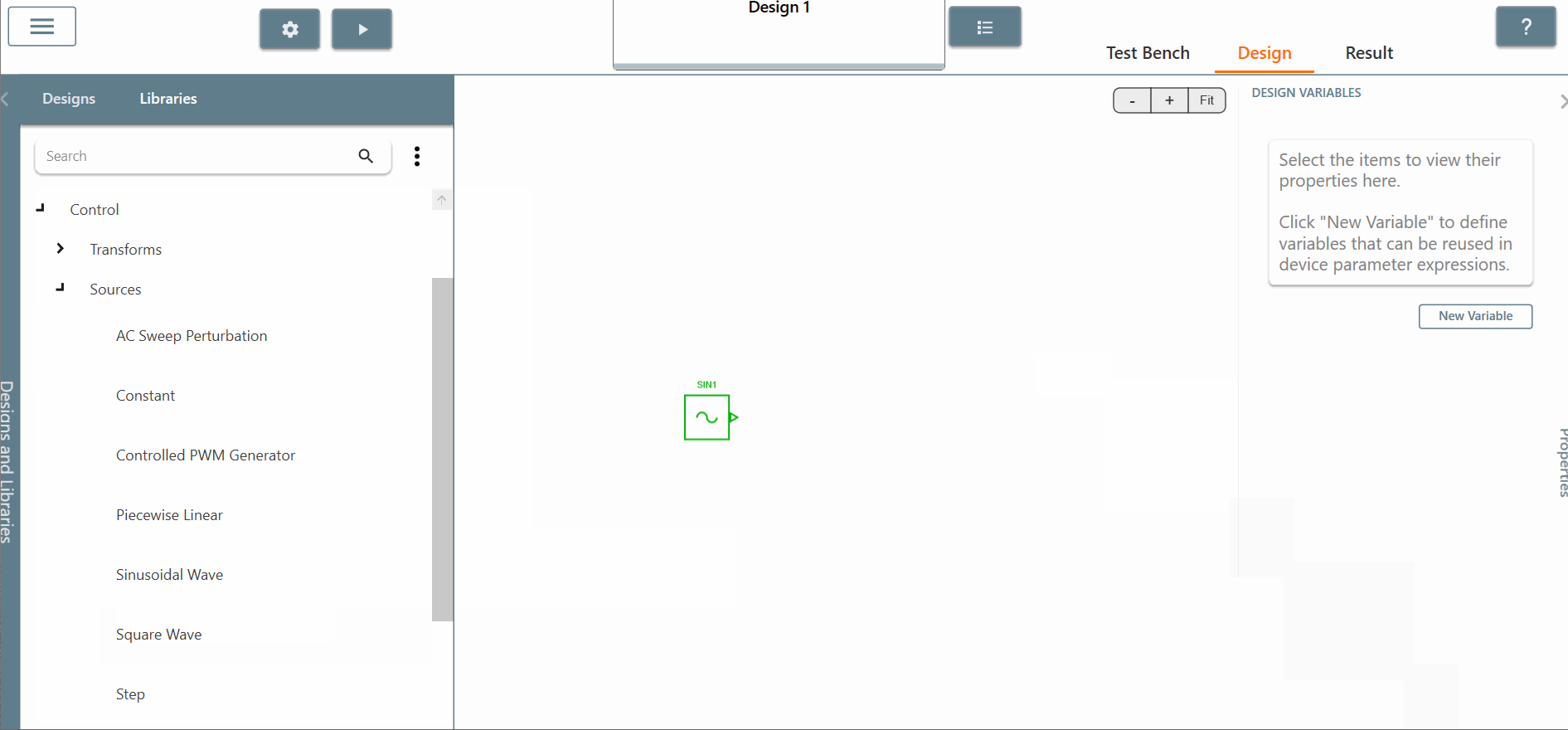
stable

✔ Step 2.b: Choose and place the "C block" and connect it directly to the sinusoidal source. Check the box for both input and outputs scopes of the C block to see the results.

run

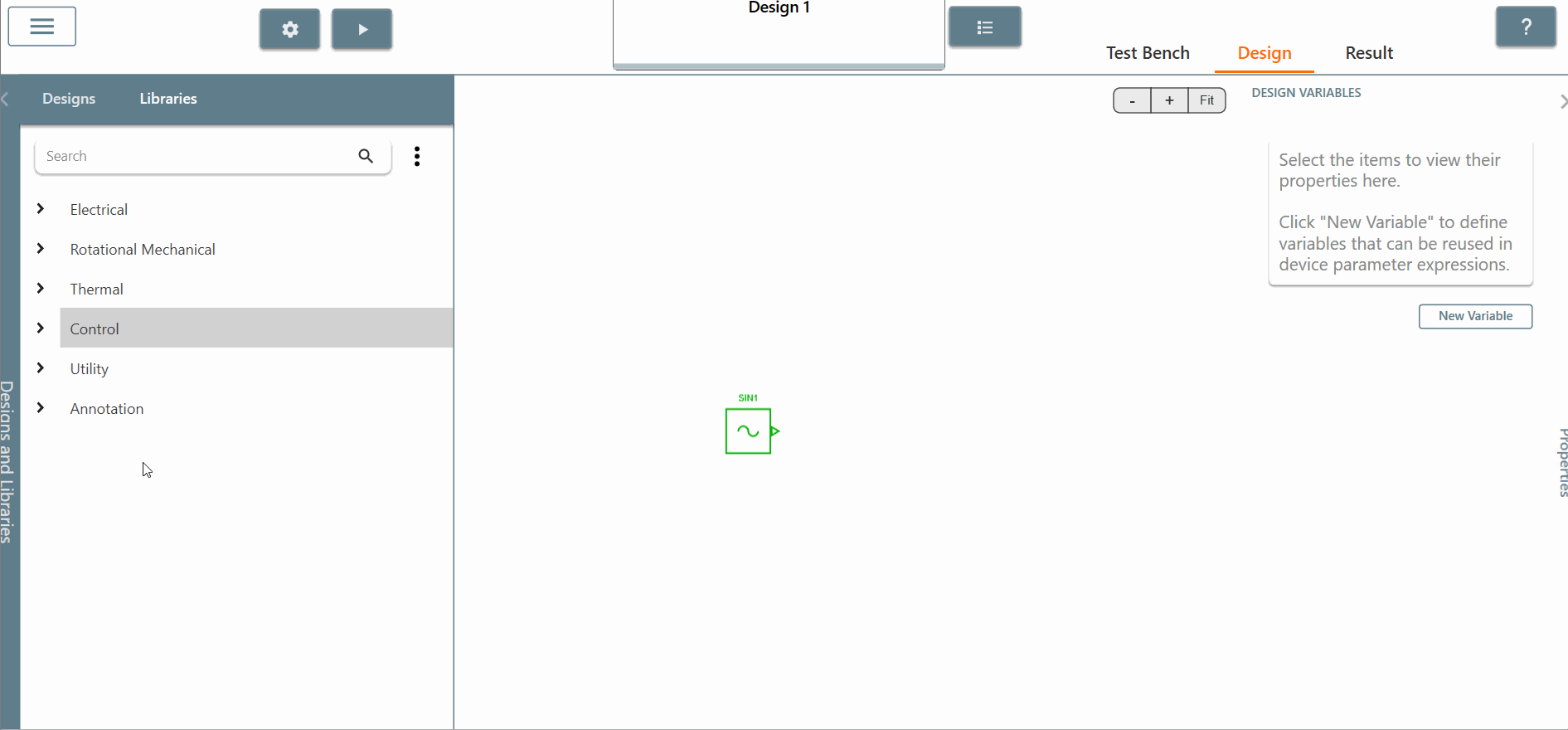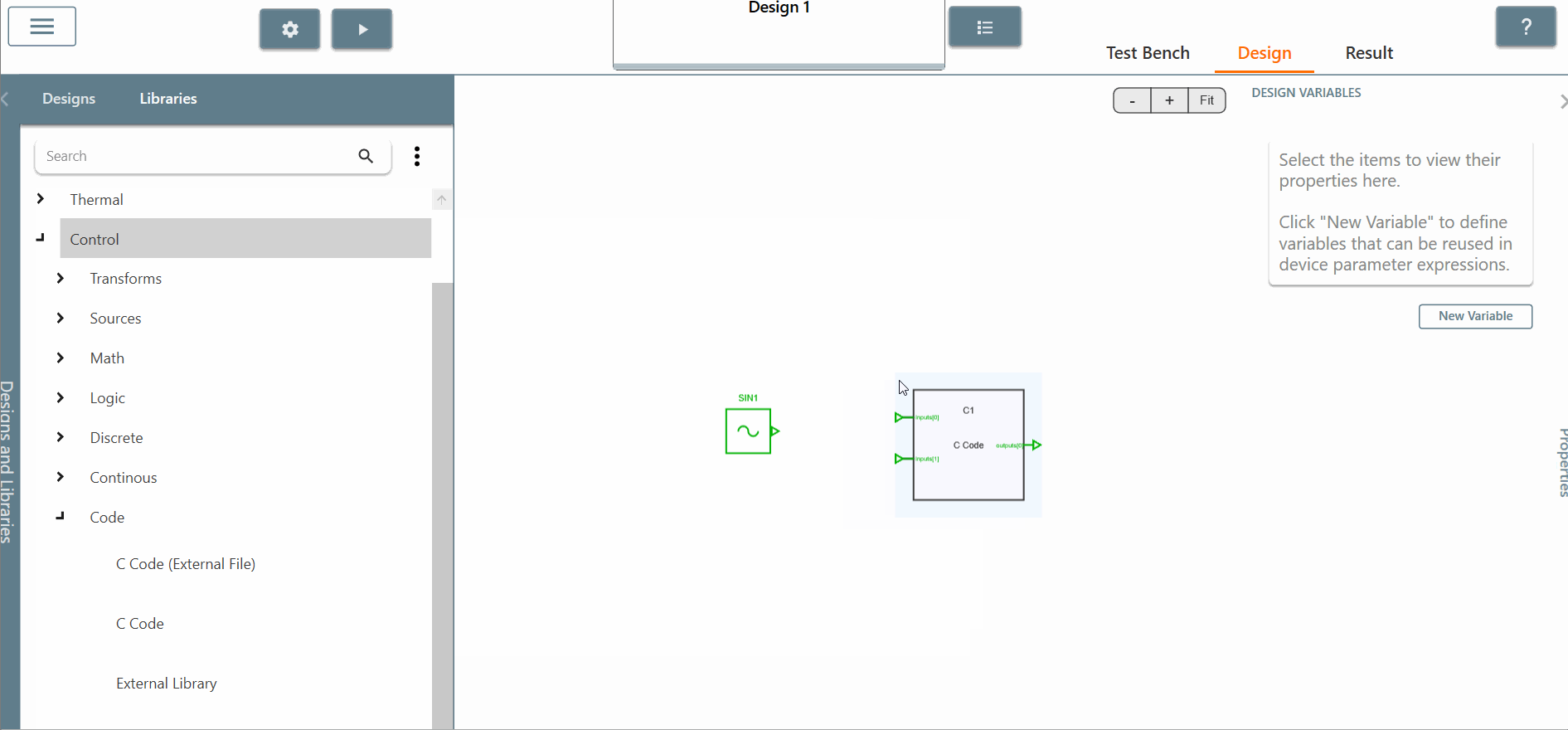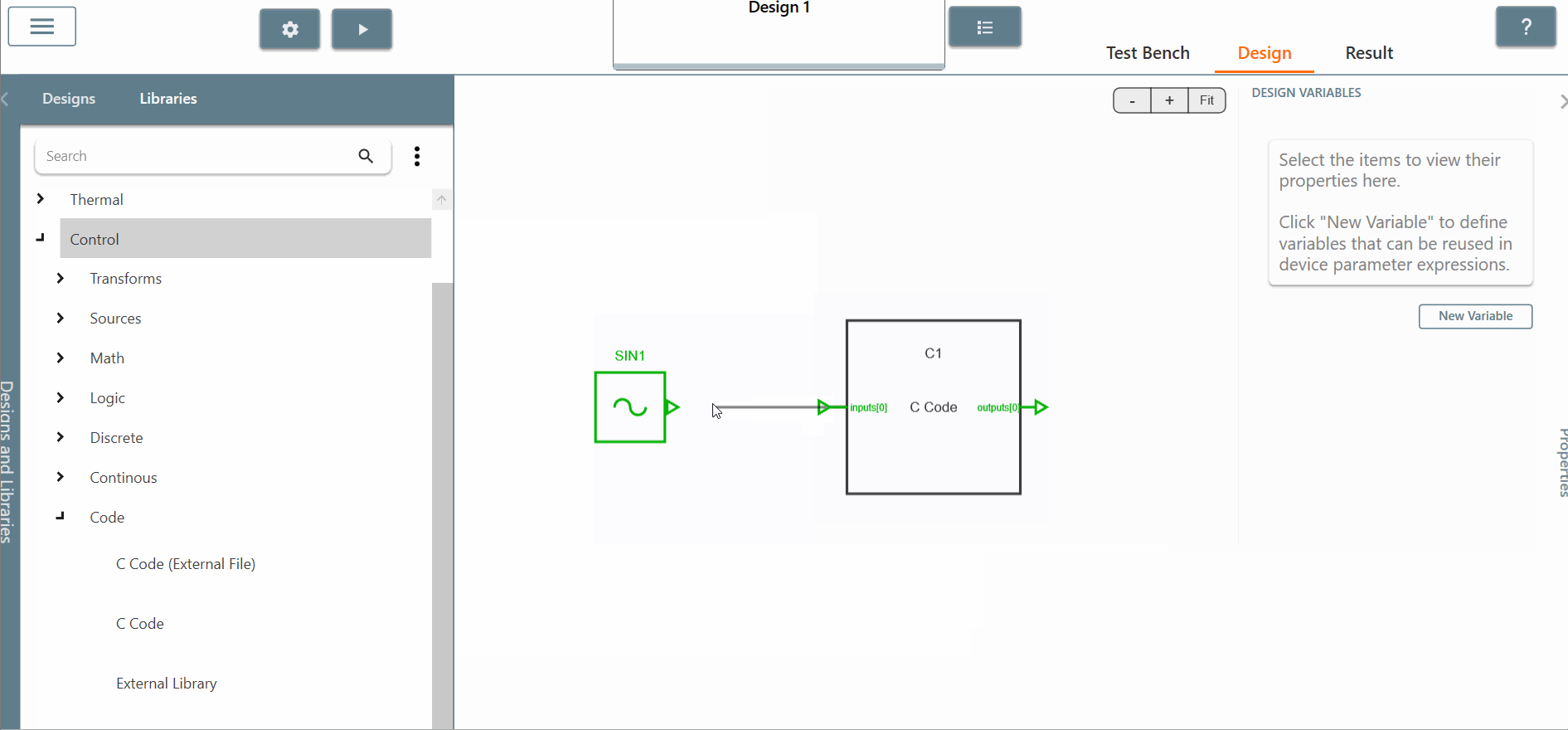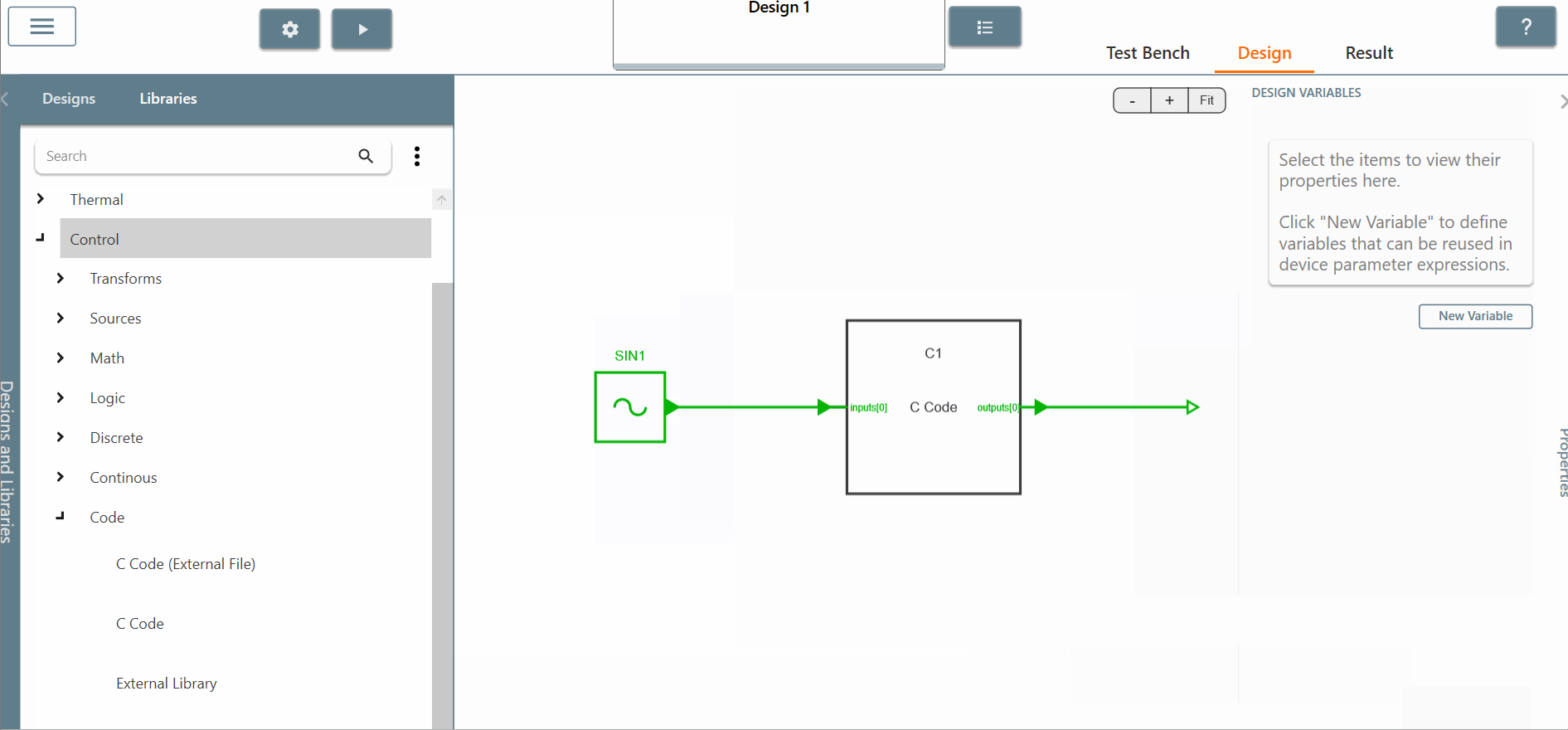
✔ Step 2.c: Edit the "C block" and add the lines of C code for the RMS value calculation. To do this, you will need to:

  • declare code variables in the "model_data" structure.

  • initialize the code variables in the "initialize" section. We need to set it to 0 for each variable.

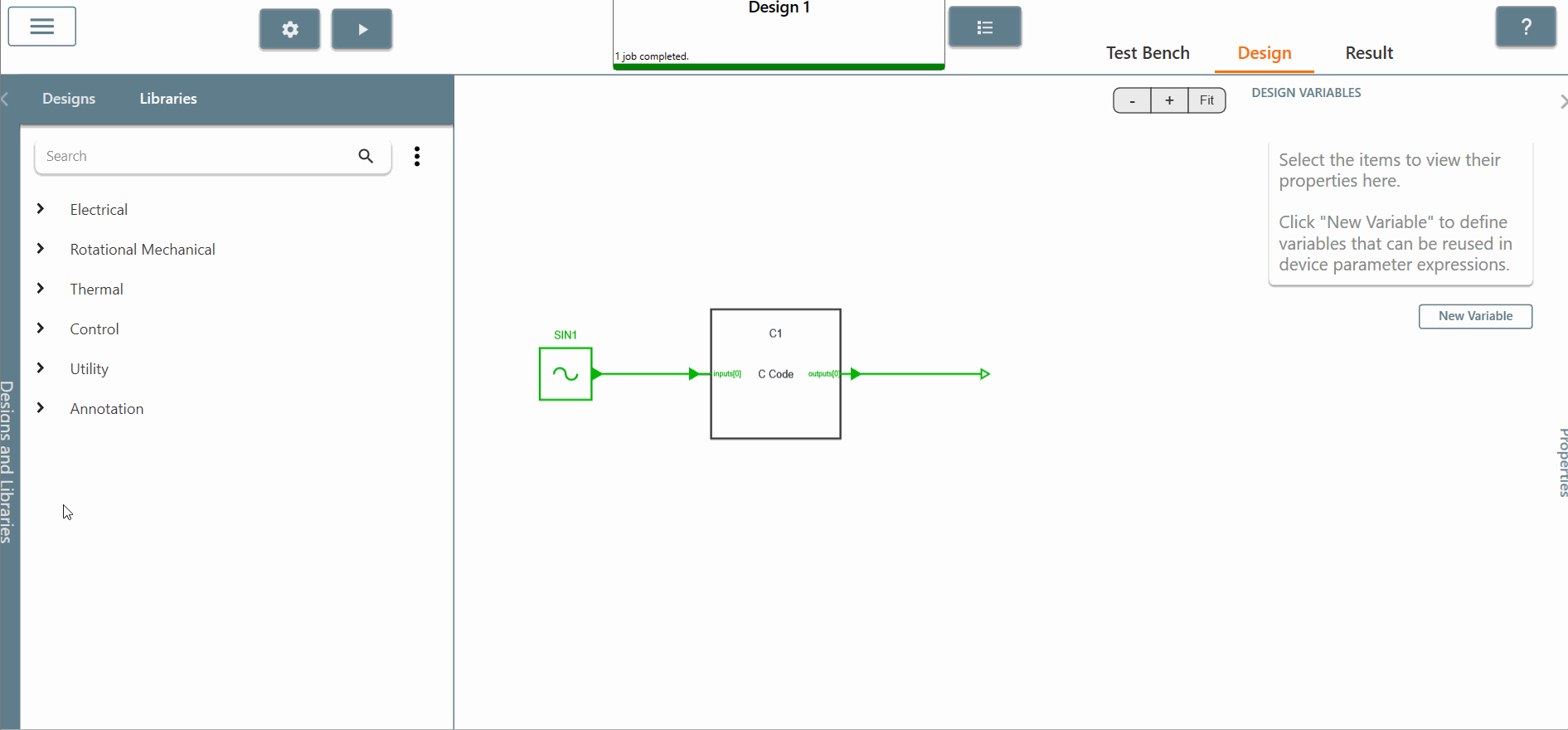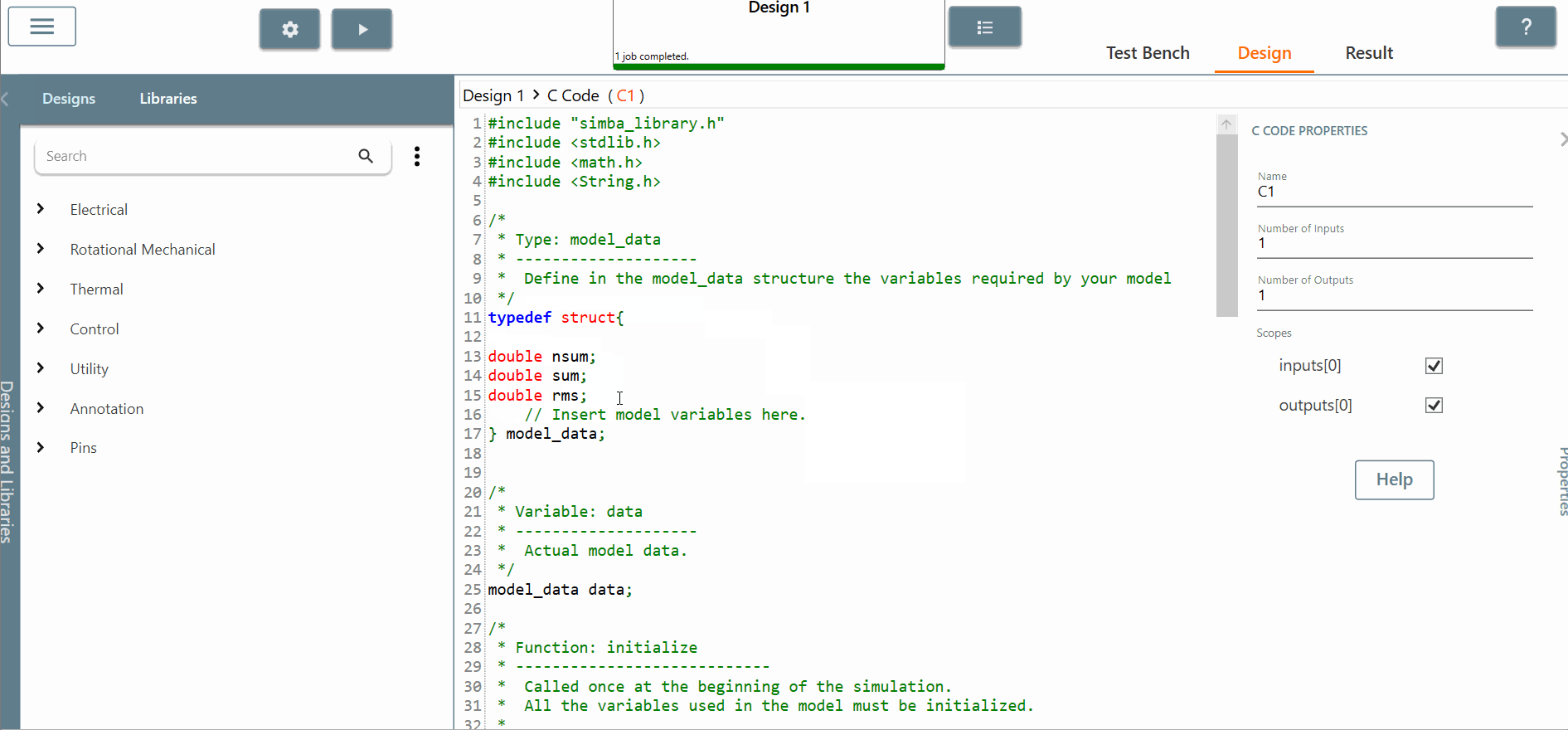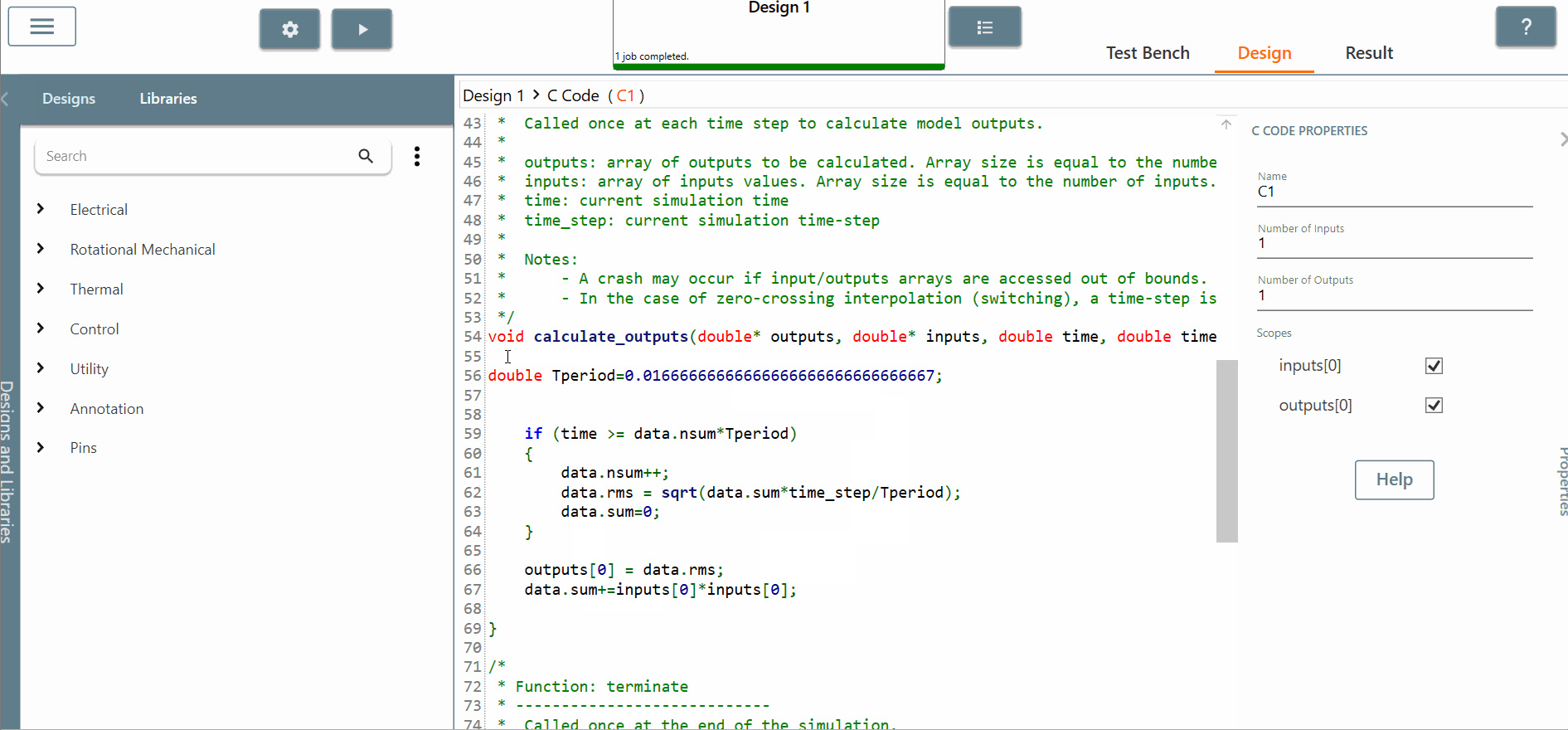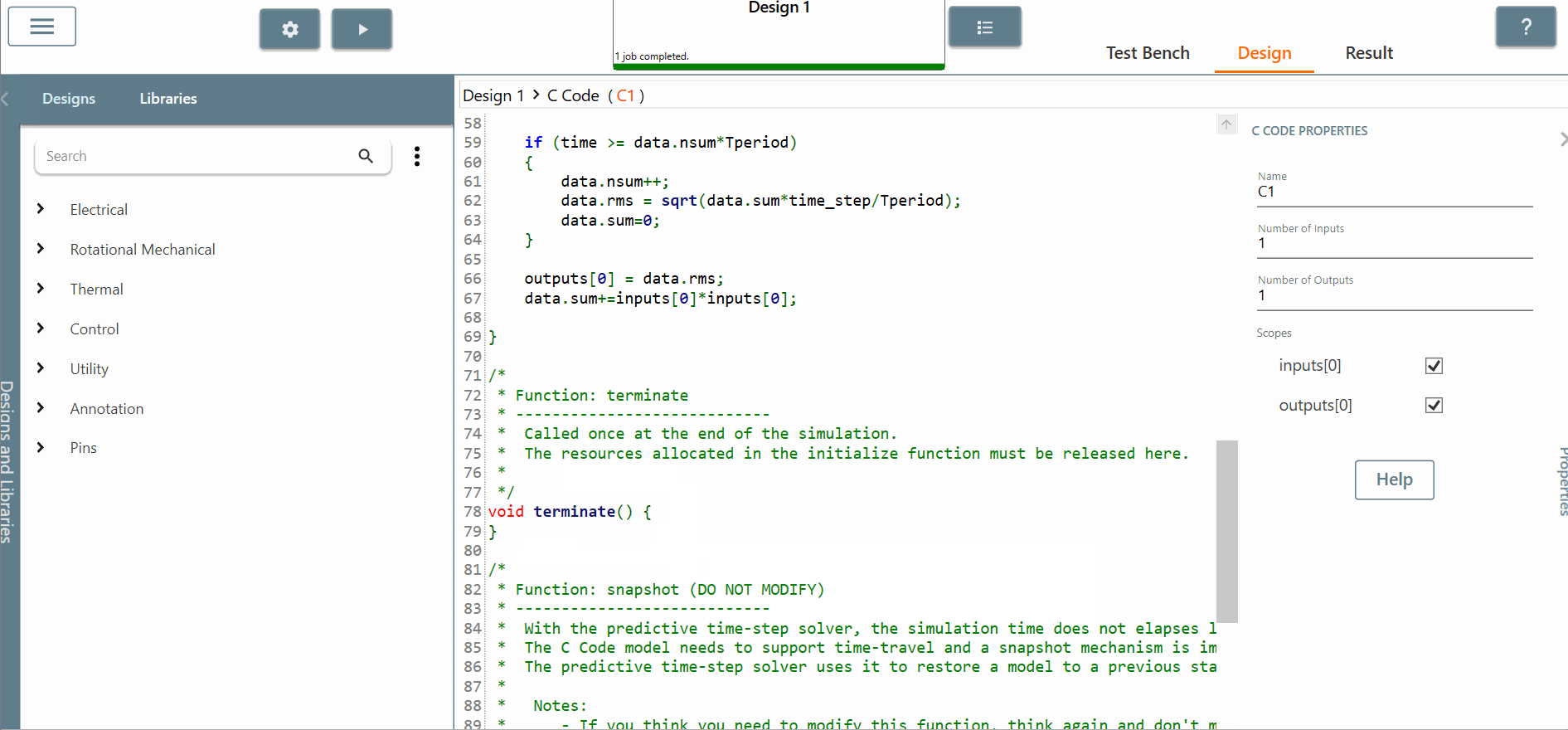
  • In the "calculate_outputs" method, you will have to add the code necessary to calculate the RMS value.

For this, you must know exactly the C code you want to implement.

  • We can leave the "terminate" function empty because we don't need to use this function in this example.

You can find more information about "C code" in the SIMBA documentation, in the section C code overview.

run

✔ Step 3: Let's run the simulation. As you can see in the "progress bar", it doesn't take long to run the circuit.

run

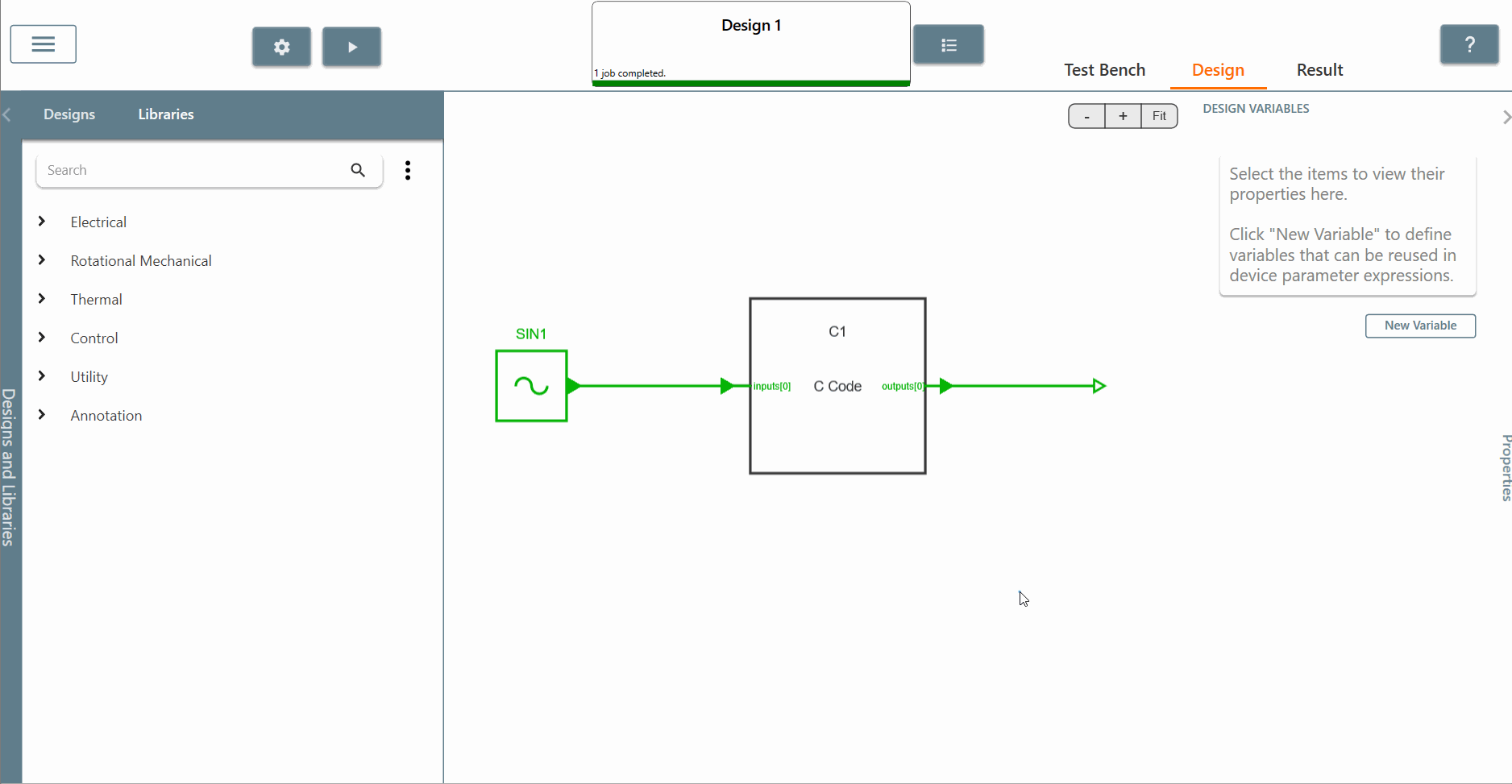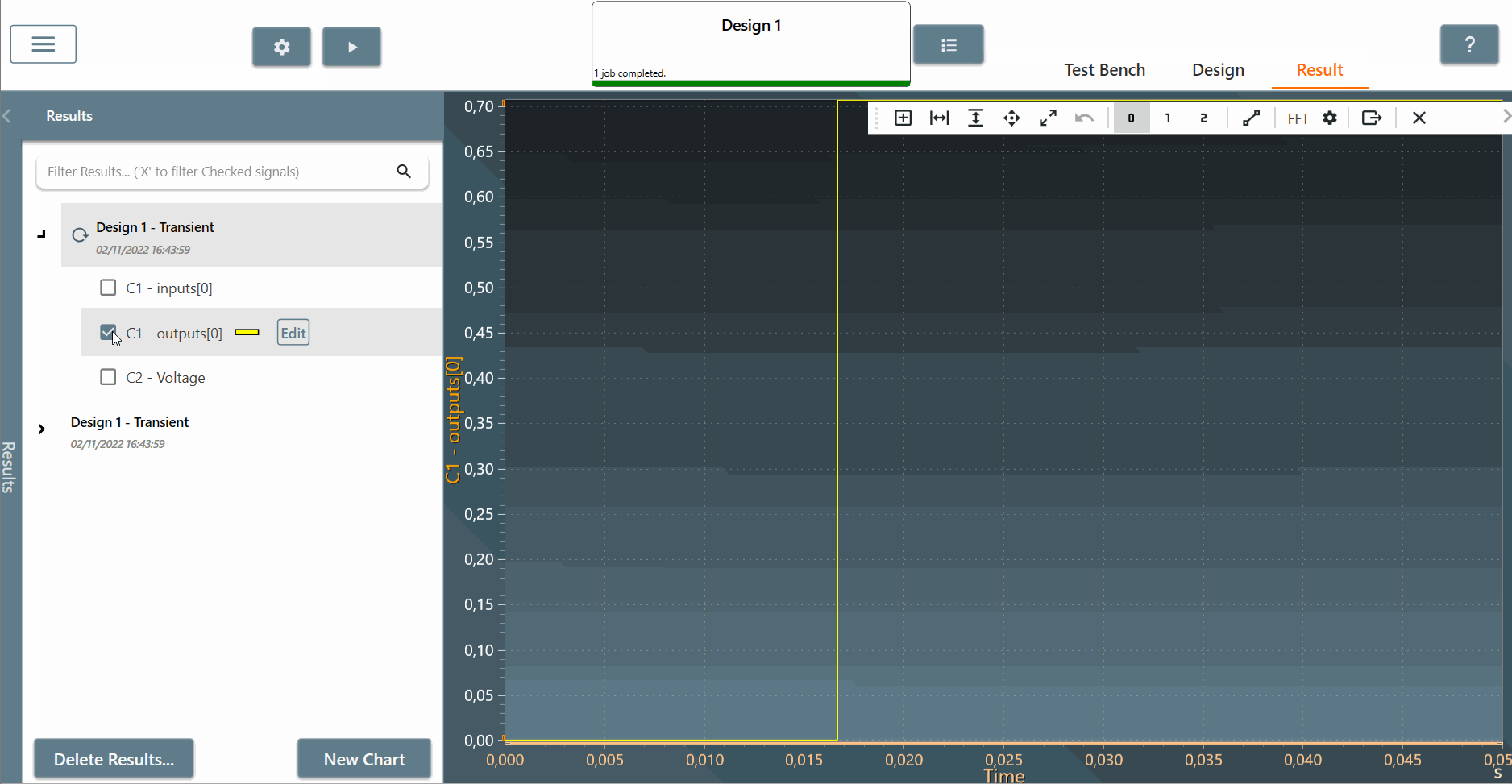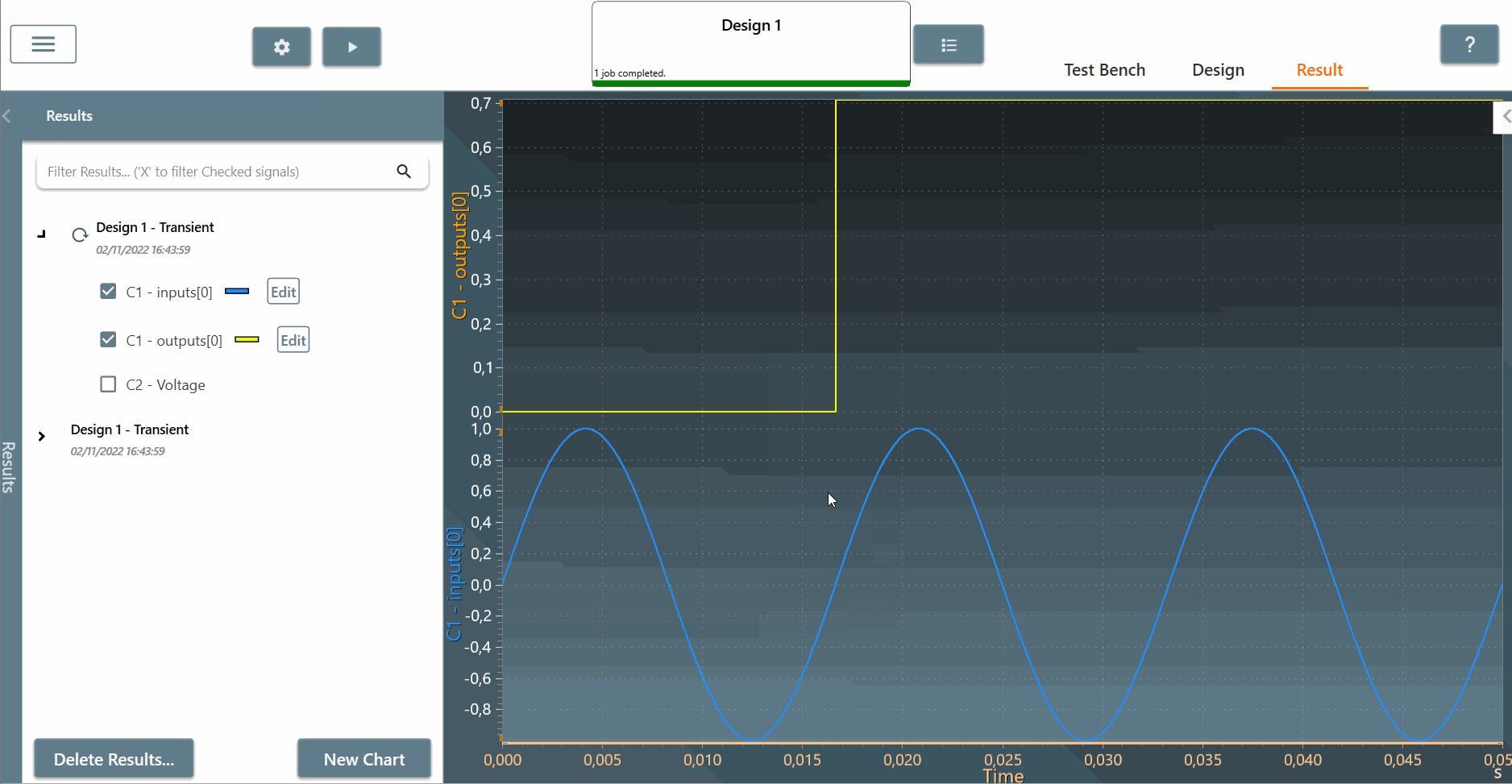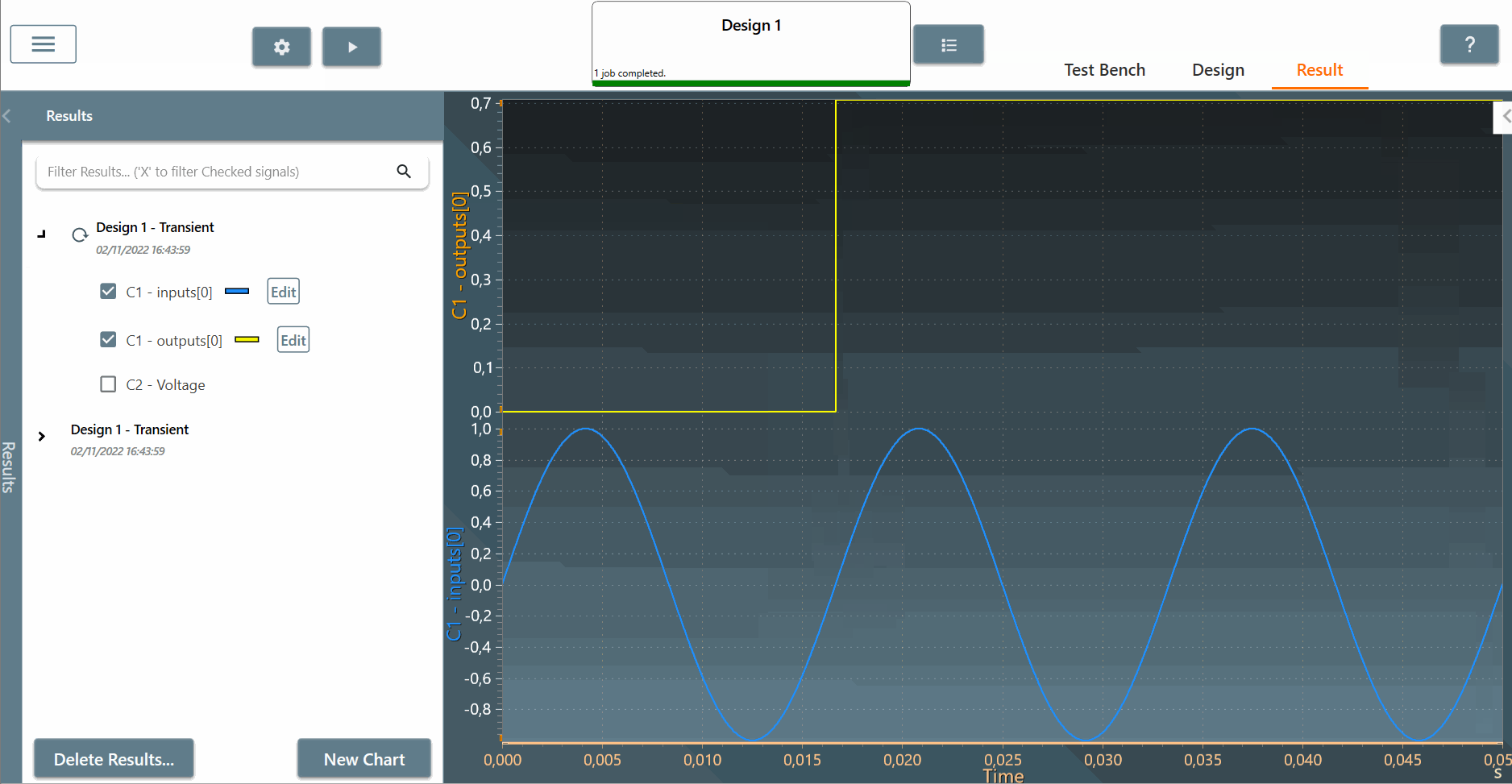
✔ Step 4: After running the simulation, we can now see the result of the RMS output in the "result" tab. Click on "C1 - outputs[0]" and the signal is equal to 0.7 after the first input period. Compare with the mathematical equation for a sinusoidal waveform:

V_{rms} = \frac{V_{max}}{\sqrt2} = \frac{1}{\sqrt2} = 0.7

We can conclude that the simulation and the mathematical equations give the same results as expected.

run

This concludes this video tutorial on the C-Code block functionality of SIMBA.