Induction machine drive example with a V / f scalar control

This example shows a induction machine supplied with a PWM inverter and driven with a $V / f$ scalar control, with:

a dc bus voltage of 600 V,
a switching frequency of 10 kHz,
a variable load torque with a square-law characteristic (such as booster pumps and centrifugal fans), with $T_{load} = 0.1 + 0.003 \times \Omega^2$ .

Control structure

The diagram below shows the closed-loop $V / f$ control structure.

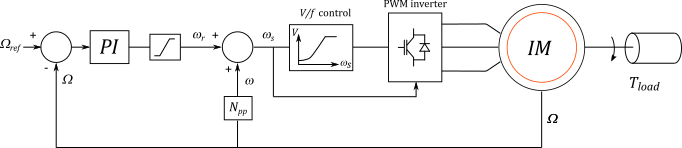
IM_V_f_control_diagram

This $V / f$ control makes possible to drive the induction machine with a constant flux (considering the stator resistance can be neglected).

Principle of the control

The electromagnetical torque of an induction machine can be given by:

$T_{em} = 3 N_{pp} \left(\frac{V_s}{\omega_s}\right)^2 \frac{R_r / \omega_r}{(R_r / \omega_r)^2 + L_r^2}$

The maximum torque - when $\omega_r = R_r / L_r$ - is then:

$(T_{em})_{max} = \frac{3 N_{pp}}{2 L_r} \left(\frac{V_s}{\omega_s}\right)^2$

$N_{pp}$ number of pole pairs
$V_s$ equivalent single-phase voltage
$\omega_s$ pulsation of the stator currents
$\omega_r$ pulsation of the rotor currents
$R_r$ rotor resistance at the stator side
$L_r$ rotor leakage inductor at the stator side

If the ratio $V_s / \omega_s$ can be kept constant, the maximum value of the torque will be constant for different synchronous speeds $\Omega_s$ . This principle is illustrated in the figure below:

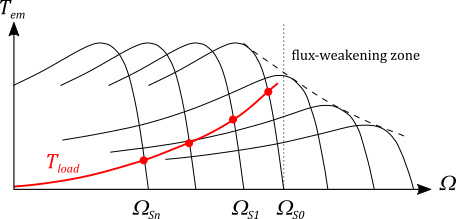
IM_Torque_Speed_V_f_constant

For low speeds, the ohmic voltage drop due to the stator resistance cannot be neglected. For high speeds, when the voltage reaches this maximum, this ratio decreases leading to a flux-weakening zone and a decreasing of the torque. This makes possible to reach higher speeds than the nominal speed.

Industrial variable speed drives propose modified $V / f$ control profiles with:

an adding term for low frequencies to keep a minimum torque,
a saturation when the voltage reaches its maximum value.

This control profile is illustrated in the global control diagram above in the $V / f$ block. Such a control profile has not been implemented in the demo example as it was not necessary.

Torque control

The torque can then be controlled with $\omega_r$ according to the first expression of the electromagnetical torque. For small values of $\omega_r$ , the torque expression can even be considered linear with $\omega_r$ :

$T_{em} \approx 3 N_{pp} \left(\frac{V_s}{\omega_s}\right)^2 \frac{\omega_r}{R_r}$

Speed loop

The speed loop involves a classic PI regulator.

Reference

This circuit example is issued from an example proposed by Christophe Haouy.