Permanent Magnet Synchronous Machine (PMSM)

Symbol

Description

Model of a three-phase Permanent Magnet Synchronous Machine (PMSM) with the sinusoidal back Electro-Motive Force (EMF). In motor operation torque and speed have the same sign. Rotor Angle is defined as the angle between the a-phase and the d-axis. In this model, the saturation can be modeled using a piecewise linear approximation of direct and quadratic axis inductances. Stator winding is star connected in this model. To access the neutral point pin, check the "Neutral Point" checkbox in the properties menu.

Electrical model and equations

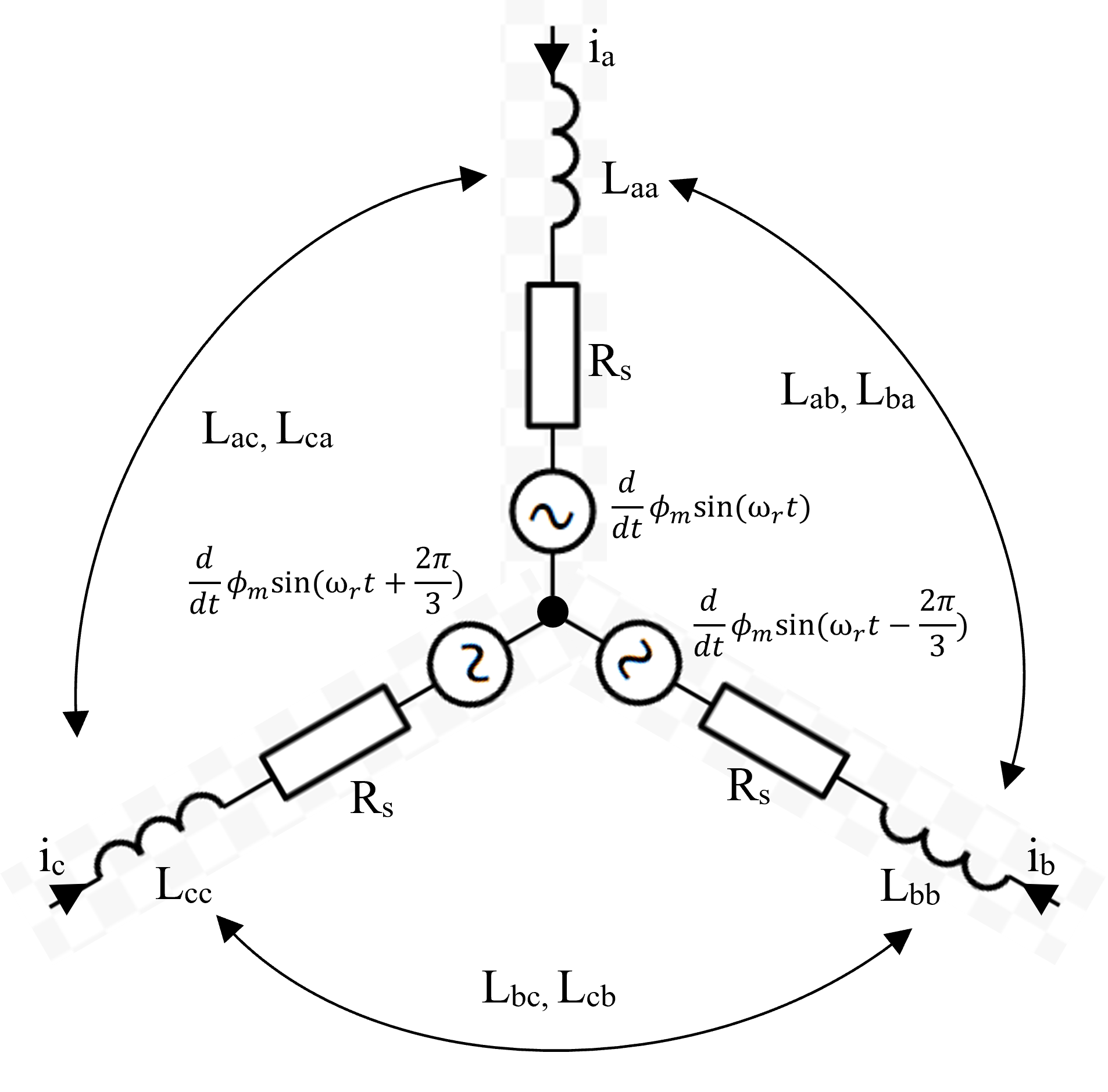
vd_vq_circuits

$v_a = R_s i_a + \frac{d}{dt} (L_{aa} i_a + L_{ab} i_b + L_{ac} i_c) + \frac{d }{dt} \phi_m \sin{(\omega_r t)}$

$v_b = R_s i_b + \frac{d}{dt} (L_{ba} i_a + L_{bb} i_b + L_{bc} i_c) + \frac{d }{dt}\phi_m \sin{(\omega_r t - \frac{2 \pi }{3})}$

$v_c = R_s i_c + \frac{d}{dt} (L_{ca} i_a + L_{cb} i_b + L_{cc} i_c) + \frac{d }{dt} \phi_m \sin{(\omega_r t + \frac{2 \pi }{3})}$

where $\phi_m = \frac{K_e}{ N_{ pp} }$ is the permanent magnet flux linkage, and $\omega_r = N_{pp} \Omega$ is the electrical speed of the rotor field. Phase inductances ( $L_{aa}$ , $L_{ab}$ , $L_{ac}$ ,..., $L_{cc}$ ) are calculated from the rotor reference frame inductance ( $L_{d}$ , $L_{q}$ ) defined in the property panel as the incremental inductance.
This component will use the lineary interpolated inductance when the current is between the two segmented points.

Electromechanical equations

Electro-magnetic torque:

$T_e = 1.5 * N_{ pp}*(i_q * \phi_d - i_d * \phi_q)$

where $\phi_d = L_d i_d + \phi_m$ and $\phi_q = L_q i_q$

Mechanical rotational speed $\Omega$ :

$J \frac{d\Omega}{ dt} = T_e - B \Omega$

Library

Electrical > Motors

Pins

Name	Description
Pin_A	Phase A (Electrical)
Pin_B	Phase B (Electrical)
Pin_C	Phase C (Electrical)
Pin_R	Rotor (Rotational Mechanical)
Pin_Angle	Rotor Angle in radians, electrical angle (Control)
Pin_N	Neutral Point (Electrical)

Parameters

Name	Description
Rs	Stator Winding Resistance [Ohm]
Ld	Direct Axis Inductance [H]
Lq	Quadratic Axis Inductance [H]
Ke	Back-EMF Constant
J	Rotor Inertia [kg.m²]
B	Rotor Friction Coefficient [N.m/(rad/s)]
InitialSpeed	Rotor initial speed [ rad/s]
NPP	Number of pole pairs
ExposeNeutralPoint	Neutral Point